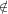3.2 k-cluster problem

Given a graph G = (V,E) the k-cluster problem consists of determining a subset S ⊆ V of k vertices such that the sum of the weights of the edges between vertices in S is maximized.

Letting n = |V | denote the number of vertices, and w_ij denote the edge weight for ij ∈ E and w_ij = 0 for ij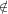E, the problem can be modeled as the following 0-1 quadratic problem:

maximize	xTWx
subject to	∑ ixi = k, x ∈{0,1}n.