3.3 Maximum independent set problem

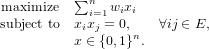
Consider an undirected graph G = (V,E), where V = {1,...,n} and |E| = m. A weight wi ∈R is assigned to each vertex i ∈ V . An independent set is a set S ⊆ V such that no two vertices in S are joined by an edge in E. We seek an independent set of maximum total weight in G.

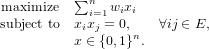
∑n maximize i=1wixi subject to xixj = 0,n ∀ij ∈ E, x ∈ {0,1} .
For this problem, we take advantage of the constraints by fixing several nodes at the same time in BiqCrunch when a decision variable is set to 1. Indeed, if (ic,j) is an edge of G and xic = 1 then xj = 0. The function BC_FixVariable (defined in problems/max-indep-set/heur.c) is used to fix additional variables whenever one variable is fixed. Note that in problems/generic/heur.c the body of this function is empty. Of course, for other problems with particular constraints, one may modify this function (as is done for the maximum independent set problem) to decrease the size of the subproblems. 
 
void BC_FixVariables(BobNode *node, int ic, int xic) { 
int j; 
 
   if (xic == 1) { 
      for (j = 0; j < BobPbSize; j++) { 
         if (j != ic) 
            if (getSparseAdjacencyMatrixValue(M_adj, ic, j) == 1.) { 
            // (ic,j) belongs to E so X[ic] = 1 => X[j] = 0 
                if(!node->xfixed[j]) { 
                node->xfixed[j] = 1; 
                node->sol.X[j] = 0; 
                } 
            } 
      } 
   } 
}
 
Code 3.1: Use of the BC_FixVariable for the MIS problem
  3.3.1 Maximum independent set heuristics